2D物理(15) LocalSpace&WorldSpace

By pocaster
Posted on May 23, 2024

本地与全局坐标系变换系统

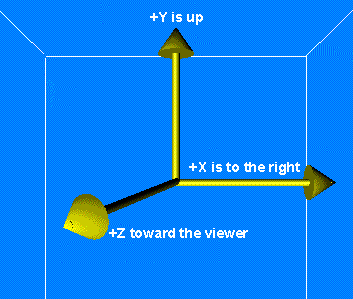
▌ 核心原理图解

1. 核心变换公式

\begin{cases}
世界坐标 = \text{Transform矩阵} \times 局部坐标 \\
\text{Transform} = \begin{bmatrix}
\cosθ & -\sinθ & x \\
\sinθ & \cosθ & y \\
0 & 0 & 1
\end{bmatrix} 
\end{cases}
Right Hand Coordinate System

I. 变换矩阵实现

1.1 数据结构设计

struct Transform2D {
    Vec2 position;   // 世界坐标位置 (x,y)
    float rotation;  // 旋转角度（弧度）
    float scale;     // 均匀缩放系数
  
    // 缓存变换矩阵（每秒自动更新）
    Matrix3x3 matrix_cache; 
    bool dirty_flag = true;
};

1.2 矩阵计算器

Matrix3x3 ComputeTransformMatrix() const {
    Matrix3x3 m;
  
    // 缩放部分
    m.m[0][0] = cosf(rotation) * scale;
    m.m[0][1] = -sinf(rotation) * scale;
    m.m[1][0] = sinf(rotation) * scale;
    m.m[1][1] = cosf(rotation) * scale;
  
    // 平移部分
    m.m[0][2] = position.x;
    m.m[1][2] = position.y;
  
    return m;
}

1.3 更新策略

void Transform2D::UpdateCache() {
    if(dirty_flag) {
        matrix_cache = ComputeTransformMatrix();
        dirty_flag = false;
    }
}

II. 坐标转换接口

2.1 点变换

// 局部 → 世界
Vec2 TransformPoint(const Vec2& local_point) {
    UpdateCache();
    return matrix_cache * local_point;  // 矩阵乘法
}

// 世界 → 局部
Vec2 InverseTransformPoint(const Vec2& world_point) {
    UpdateCache();
    return matrix_cache.Inverse() * world_point;
}

2.2 方向转换

Vec2 TransformDirection(const Vec2& local_dir) {
    return Vec2(
        cosf(rotation)*local_dir.x - sinf(rotation)*local_dir.y,
        sinf(rotation)*local_dir.x + cosf(rotation)*local_dir.y
    ) * scale;
}

2.3 矩阵分解

void DecomposeMatrix(const Matrix3x3& m, Vec2& pos, float& rot, float& scale) {
    pos.x = m.m[0][2];
    pos.y = m.m[1][2];
  
    scale = sqrtf(m.m[0][0]^2 + m.m[1][0]^2);
    rot = atan2f(m.m[1][0]/scale, m.m[0][0]/scale);
}

III. 物理量变换

3.1 力的应用

// 在局部坐标系施加力
void ApplyLocalForce(const Vec2& local_force) {
    Vec2 world_force = TransformDirection(local_force);
    force_accum += world_force;
}

// 在局部点施加力
void ApplyForceAtLocalPoint(const Vec2& force, const Vec2& local_point) {
    Vec2 world_point = TransformPoint(local_point);
    ApplyForceAtWorldPoint(force, world_point);
}

3.2 冲量响应

接触点在世界空间计算冲量后，逆向转换到局部空间进行状态修正：

Vec2 local_impulse = InverseTransformDirection(world_impulse);
// 应用局部冲量到物理状态...

IV. 碰撞检测系统

4.1 形状变换流程

graph LR
    LocalVerts[局部顶点] --> TransformMatrix[应用Transform矩阵]
    TransformMatrix --> WorldVerts[世界空间顶点]
    WorldVerts --> SAT[分离轴检测]

4.2 边界更新逻辑

void Shape::UpdateWorldBounds() {
    Transform& tf = body->transform;
  
    // 对于凸多边形
    for(int i=0; i<local_verts.size(); ++i) {
        world_verts[i] = tf.TransformPoint(local_verts[i]);
    }
  
    // 重新计算AABB
    world_aabb = CalculateAABB(world_verts);
}

V. 相对运动处理

5.1 相对速度计算

// 计算点在世界空间的绝对速度
Vec2 GetWorldVelocityAtPoint(const Vec2& world_point) {
    Vec2 r = world_point - position;
    return linear_vel + Vec2(-r.y, r.x) * angular_vel; // v + ω×r
}

5.2 多刚体相对观察

计算B相对于A的相对运动：

void ComputeRelativeMotion(const RigidBody& a, const RigidBody& b) {
    // 相对线速度：v_B - v_A
    relative_linear_vel = b.linear_vel - a.linear_vel;
  
    // 相对角速度：ω_B - ω_A
    relative_angular_vel = b.angular_vel - a.angular_vel;
}

VI. 变换优化技巧

6.1 四元数优化（3D准备）

struct Transform3D {
    Quaternion rotation;  // 使用四元数替代欧拉角
    Vec3 position;
    float scale;
  
    mutable Matrix4x4 cached_matrix;
};

6.2 变换层级系统

class TransformTree {
    TransformNode* root;  // 根节点
    unordered_map<EntityID, TransformNode*> node_map;
  
    void UpdateHierarchy() {
        // 广度优先更新变换树
    }
};

6.3 异步更新策略

const float TRANSFORM_UPDATE_INTERVAL = 0.1f; // 10Hz
float update_timer = 0;

// 在游戏循环中：
update_timer += delta_time;
if(update_timer >= TRANSFORM_UPDATE_INTERVAL) {
    UpdateAllTransforms();
    update_timer -= TRANSFORM_UPDATE_INTERVAL;
}

VIII. 调试可视化

7.1 坐标系绘制

void DebugDraw::DrawLocalAxes(const Transform& tf) {
    Vec2 origin = tf.position;
    Vec2 x_axis = tf.TransformDirection(Vec2(1,0));
    Vec2 y_axis = tf.TransformDirection(Vec2(0,1));
  
    DrawArrow(origin, origin + x_axis, RED);  // X轴
    DrawArrow(origin, origin + y_axis, GREEN);// Y轴
}

7.2 碰撞形状比较

// 同时绘制局部和世界网格对比
void DrawColliderDebug() {
    DrawPolygon(local_verts, BLUE);     // 局部坐标系轮廓
    DrawPolygon(world_verts, YELLOW);   // 世界坐标系轮廓
}

IX. 实用工具方法

8.1 屏幕空间转换

Vec2 WorldToScreen(const Vec2& world_pos, const Camera& cam) {
    Matrix3x3 view_matrix = cam.GetViewMatrix();
    return view_matrix * world_pos;
}

Vec2 ScreenToWorld(const Vec2& screen_pos, const Camera& cam) {
    Matrix3x3 inv_view = cam.GetInvViewMatrix();
    return inv_view * screen_pos;
}

8.2 运动学约束

保留物体的局部坐标关系：

void MaintainRelativePosition(Entity& parent, Entity& child) {
    Transform ptf = parent.GetTransform();
    Transform ctf = child.GetTransform();
  
    // 保持相对位移不变
    Vec2 new_child_pos = ptf.TransformPoint(child.local_pos);
    child.SetWorldPosition(new_child_pos);
}

X. 常见问题分析

现象 根本原因 解决方案
物理形状错位 变换未及时更新 强制标记dirty_flag并重新计算
碰撞检测失效 未正确更新世界坐标系顶点 添加碰撞阶段形状更新回调
旋转后出现抖动 累积矩阵计算误差 定期矩阵正交化处理
层级变换产生撕裂 多级变换顺序错误 使用广度优先变换更新策略

设计原则总结

  1. 分层解耦：物理模拟只关注世界坐标系，图形显示处理局部坐标系细节
  2. 逆可逆性：所有变换必须支持逆向计算（World→Local）
  3. 状态一致性：确保物理属性和变换矩阵之间的同步
  4. 性能预判：利用空间划分技术降低转换计算量
Tags: Gamedev Public AI